Доверительный интервал для математического ожидания позволяет оценить диапазон, в котором с заданной вероятностью находится истинное среднее значение генеральной совокупности. Рассмотрим методы построения доверительных интервалов для разных условий.
Содержание
Основные понятия
- Доверительный уровень (1-α) - вероятность попадания истинного значения в интервал
- Точечная оценка - выборочное среднее (x̄)
- Стандартная ошибка - мера изменчивости оценки
- Критическое значение - величина из распределения Стьюдента или нормального
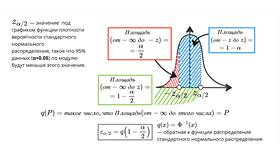
Формула доверительного интервала
| Общий вид | x̄ ± tα/2 * (s/√n) |
| Где: |
|
Пошаговый алгоритм построения
- Вычислите выборочное среднее (x̄)
- Определите стандартное отклонение выборки (s)
- Выберите доверительный уровень (обычно 95%)
- Найдите критическое значение t-распределения
- Рассчитайте стандартную ошибку: SE = s/√n
- Вычислите предельную ошибку: ME = t * SE
- Постройте интервал: x̄ ± ME
Выбор распределения
| Условия | Используемое распределение |
| n > 30 или известно σ генеральной совокупности | Нормальное (z-распределение) |
| n ≤ 30 и σ неизвестно | t-распределение Стьюдента |
Пример расчета
Для выборки из 25 элементов с x̄ = 50, s = 10 и доверительным уровнем 95%:
- Степени свободы: df = n-1 = 24
- t-критическое (α=0.05, двусторонний): 2.064
- Стандартная ошибка: 10/√25 = 2
- Предельная ошибка: 2.064 * 2 ≈ 4.128
- Доверительный интервал: 50 ± 4.128 → (45.872, 54.128)
Факторы, влияющие на ширину интервала
- Объем выборки (n) - обратная зависимость
- Доверительный уровень - прямая зависимость
- Изменчивость данных (s) - прямая зависимость
Практические рекомендации
- Для малых выборок всегда используйте t-распределение
- Проверяйте предположение о нормальности распределения
- При больших выборках (n>100) z и t дают близкие результаты
- Для пропорций используйте другие формулы доверительных интервалов